指令调度 - Amethyst Studio

基本问题#

观察如下的代码（取自鲸书）：

r2 <- [r1](4)
r3 <- [r1+4](4)
r4 <- r2+r3
r5 <- r2 - 1
goto L1
nop

流水线#

现代处理器在执行指令时是采用流水线方式。举一个例子，经典的流水线方式，把一个指令的执行分成了取指，译码，执行，访存，写回。假设这五个步骤都耗费一个时钟周期，那么当第一条指令完成了取指，进入译码阶段的时候，第二条指令开始了取指；当第一条指令完成了译码，进入执行阶段的时候，第二条指令同时完成了取指，进入译码阶段，而后第三条指令开始了取指。

但是这里有一个问题，如果第二条指令使用到了第一条指令的结果，那么会出现什么问题？

例如下面的代码：

r2 <- [r1](4)
r3 <- r2 + 1

在这种情况下，第二条指令就不得不等待第一条指令执行完毕之后再去执行，这样就出现了流水线打断的问题。

回到一开始的例子：

r2 <- [r1](4)
r3 <- [r1+4](4)
r4 <- r2+r3
r5 <- r2 - 1
goto L1
nop

这个例子中，第一二条指令涉及到了访存，假定需要两拍，其余指令假定需要一拍，此时，由于第一二条指令没有依赖关系，因此利用到了流水线，但是第三条指令要用到第二条指令的结果，因此出现了流水线打断的问题，因此第一二条指令耗时三拍，然后执行后面的四条指令，总共4拍。

但是只要稍微调整一下这个代码的结构，让第三四条指令换个位置：

r2 <- [r1](4)
r3 <- [r1+4](4)
r5 <- r2 - 1
r4 <- r2+r3
goto L1
nop

这样一来，第三条指令可以在时间为2拍的时候顺利进入流水线，第四条指令可以在时间为3拍的时候进入流水线，于是前4条指令就只需要4拍，整个程序就变成了6拍。

延迟槽#

许多体系结构下，在分支指令和调用指令之后，存在一个延迟槽。具体来说，在执行分支指令的时候，pc指针并没有立刻指向目的地，而是延迟了一会才将pc指针指向目的地。延迟槽一般有两种，一种是分支指令延迟槽，一种是调用指令延迟槽。上面的代码中。这个延迟槽的存在实际仍与处理器流水线有关。我们前面说goto和nop各用1拍的时间，其实是不对的，应该说，goto占用2拍的时间，但是1拍后，nop开始执行。而nop用时1拍。goto和nop共占2拍。 goto之后的指令，实际上处于延迟槽当中，考虑到处于延迟槽中的是nop，其实可以把这个nop给换成一个更有意义的指令，上面更新后的代码中，可以考虑把第4条指令挪到goto之后的延迟槽中，于是代码就变成了：

r2 <- [r1](4)
r3 <- [r1+4](4)
r5 <- r2 - 1
goto L1
r4 <- r2+r3

再次提醒，虽然r4的计算指令位于goto的后面，但是它处在goto后的延迟槽内，它的执行，在goto指令开始执行到程序跳转完成这么一段时间内。

代码这么变换之后，就只需要5拍了，相较与原先的代码，加速了接近 $30\%$ 。

分支调度#

分支调度要解决的问题，就是找一条指令填充分支指令或者调用指令之后的延迟槽。鲸书上有关分支调度说得更详细一点，因为不同的体系结构下，对于延迟槽的规定略有不同，例如有些体系结构允许延迟槽中的指令设定一个作废位（nullification），这样当分支跳转到预想之外的位置时，可以作废延迟槽中的指令。我这里的笔记对于作废位的问题只做简单的记录。

首先我们要考虑的问题是，什么样的指令可以填充到延迟槽里面。实际上标准很简单，一个基本的标准是，它首先不能是分支指令，其次它不可以与分支指令有依赖关系。譬如，如果一条指令影响分支指令的地址计算，那么这条指令自然就不适合放到延迟槽里面。当然这样一来，适合的指令会有很多，那我们就选择那种执行起来，其时间最接近分支指令延迟时间的指令。如果延迟槽持续1拍，那么所填充的指令最好也是一拍。不过额外注意一点的是，如果延迟槽中的指令，执行时间超过了分支指令的延迟时间，处理器实际上会发生一个停顿，会等待这条指令执行完毕后再接着执行分支跳转目的地的第一条指令。

接下来考虑怎么选这条指令。首先是考虑从分支指令所属的基本块当中选，如果这个基本块内就有符合条件的指令，那么直接用这条指令去填充延迟槽就好。

如果分支所属的基本块当中没有合适的指令，那么就从分支指令的多个后继基本块当中选择，看分支指令后面的多个后继是否会有一个公共的指令，如果有，就用这个公共的指令填充延迟槽。一般而言，这样的公共指令很可能不存在，因为指令调度一般是优化的最后一步，如果真的存在这样的公共指令，很可能在前面的优化过程中（例如LCM）给挪动过了。

如果体系结构允许我们设置作废位（nullification），那么我们还可以接着进行讨论。可以从分支的多个后继基本块中选择一个合适的指令 $J$ ，这个指令 $J$ 可能只在一个分支内，其它分支没有这个指令，但是通过设定作废位，让我们在进入其它的分支时，不真的执行指令 $J$ 。

但是，如果体系结构不允许我们设置作废位，是否意味着我们真的就不能把指令 $J$ 放到延迟槽里面？其实是未必的，如果指令 $J$ 不影响其它分支块的运转，那么其实把 $J$ 放到延迟槽里面也未尝不可。此时不管进入到那个分支， $J$ 都会被执行，但是如果进入到原本 $J$ 所在的分支块内，那自然没有什么问题。如果进入到了其它分支里面去，也不会有什么问题，因为我们这里限定了 $J$ 的执行对其它分支不起作用。

如果这样还是找不到一条合适的指令，那么就只能选择填充nop了。

基本块内的调度（表调度）#

现在，我们针对某一个基本块内进行指令调度，前面我们已经讨论过了分支指令的调度，现在假定我们已经不需要处理分支指令了，我们只针对无分支指令的基本块进行指令调度。

首先我们需要根据硬件体系结构特征，来获取每条指令的延迟时间。额外说一句，鲸书上面经常使用”拍”这种词汇来衡量一个时间周期，实践中自然需要更精准地使用”时钟周期”或者”机器周期”这样的词汇。但是这里我们还是延续了鲸书的说法，因为具体使用哪种时间衡量方法是需要具体情况具体分析的，而我们的算法是需要抽象的。

首先我们的算法需要获取基本块内指令的DAG，然后我们就是根据这个DAG来进行一个拓扑排序。而排序的依据是指令的延迟。

我们使用编号 $n$ 来代指每个指令，然后这里我们先定义两组变量：

\begin{aligned} Delay(n) &\text{ : 指令n从取指开始到基本块结束的时间}\\ ExecTime(n) &\text{ : 指令n从取指开始到执行结束的时间} \end{aligned}

对于DAG图而言，图中的每个节点都是一条指令，用 $n$ 来代指每条指令。 $ExecTime(n)$ 是现有的，现在遍历这个DAG图，来获取每个节点的 $Delay(n)$ 。

基本的思路就是一个公式：

Delay(n) = \left\{ \begin{aligned} &ExecTime(n) &\text{ if } n \in leaf(DAG) \\ &\underset{m\in succ(n)}{max}LateDelay(n,m) &\text{ if } n \notin leaf(DAG) \end{aligned}\right.

其中：

LateDelay(n, m) = Latency(n, 2, m , 1) + Delay(m)

这里的 $Latency(n, 2, m , 1)$ 指的是指令n在在进行到第2个时钟周期时，开始执行指令m的第1个时钟周期所需要等待的时间。这个是鲸书上的说法，其实可以简单地理解为，当m指令开始执行时，n指令早于m指令多长时间执行。

例如我们有如下的DAG图：

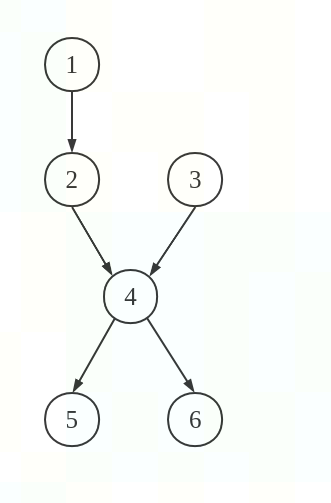
并且除指令6需要两拍 $ExecTime(6) = 2$ 外，其余都只需要1拍，那么根据上面的公式，可以很快计算出：

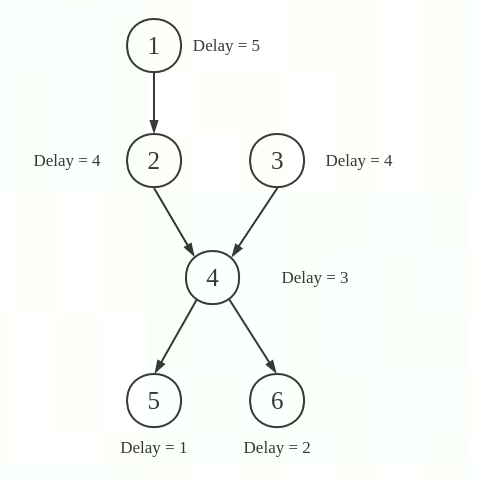
计算出每条指令的delay之后，接着就可以根据这个信息来进行拓扑排序。

（额外说明，鲸书上的这个算法应该没问题，但是后面给的例子实际上是不对的）

算法的核心思想是，每次调度的时候，优先选择那些最高延迟的指令进行调度，如果不止一个，就选那些早已就绪的指令进行调度。

算法：

Procedure Schedule(DAG):
    sched = []
    Cands = Roots(DAG)
    Delay = Compute_Delay(DAG)
    for n in Nodes(DAG) : // ETime 指明每个节点最早可以被调度的时间
        ETime[n] = 0      // 开始时置为0是为了方便根节点的ETime赋值
  
    CurTime = 0
    while Cands is not empty:
        MaxDelay = -inf  // 当前候选指令中，最大延迟时间
        for m in Cands:
            MaxDelay = max(MaxDelay, Delay(m))
        MCands = []
        ECands = []
        for m in Cands:
            if Delay(m) == MaxDelay : MCands.add(m)  // 恰好等于最大延迟时间的候选指令
        for m in MCands:
            if ETime[m] <= CurTime :  ECands.add(m)  // 上面候选指令中，早已就绪的指令
        
        if |ECands| == 1 :               // 优先调度早已就绪的指令
            let n = ECands[0]
        else if |MCands| == 1 :
            let n == MCands[0]
        else if |ECands| > 1 :           // 如果不止一个，就需要利用启发式算法选择
            let n == Heuristics(ECands)
        else
            let n == Heuristics(MCands)
        
        Sched.append(n)
        Cands.remove(n)
        CurTime += ExecTime(n)
        for i in DagSucc(n):
            hasSched = true;  //  如果i的所有前驱都已经被调度，那么才将i加入进Cands
            for j in DagPred(i):
                hasSched  = hasSched && (j in Sched)
            if hasSched:
                Cands.add(i)
            // 这里有点疑问，鲸书上max的第一项是ETime[n]，如果是ETime[n]的话
            // 就会让所有ETime都为0，因为根节点是0。
            ETime[i] = max(ETime[i], CurTime + Latency(n, 2, m , 1)) 
    return Sched

举个例子，利用前面的DAG图（注意，这里）：

开始时，CurTime = 0, Cands = {1, 3}, Sched = [], 且对所有结点n，有ETime[n] = 0, MaxDelay = 5（注意，鲸书上这里是不对的，鲸书上说得是4，导致后面整个都有一点问题）， MCands = ECands = {3}。
结点1被选上，Sched = [1], Cands = {2, 3}, CurTime = 1, ETime[2] = 1，MCancds = {2, 3}, ECands = {2, 3}
此时结点2,3都可以选，假定我们选择3，那么Sched = [1,3], Cands = {2}， CurTime = 2, ETime[4] = 3。
再把节点2调度进来，此时Sched=[1,3,2], Cands = {4}, CurTime = 3, ETime[4] = 4。
再调度进结点4，于是Sched = [1,3,2,4]，Cands = {5, 6}, CurTime=4, ETime[5] = ETime[6] = 5, MaxDelay = 2, MCands = {6}
因为|MCands| = 1，调度6，得到Sched = [1,3,2,4,6], Cands = {5}, CurTime = 5。
调度5，最终得到调度序列：Sched = [1,3,2,4,6,5]，总共需要6拍周期。